Exercise 19.4

Exercise 19.4#

Comparison of RK2, RK4, Gauss–Legendre (s=2), and Radau IIA (s=2)

Overall Process#

  1. Implementation of a generic ExplicitRungeKutta time-stepper

Created ExplicitRungeKutta class in explicitRK.hpp that takes an arbitrary Butcher tableau.

((A,b,c)) with strictly lower triangular (A) (explicit RK).

  1. Definition of specific Butcher tableaus Added setup routines for

    • RK2 (Heun)

    • RK4 (classical 4th-order)

    • Gauss–Legendre IRK (s=2)

    • Radau IIA IRK (s=2)

  2. Comparison driver

① Implemented Rk_compare.cpp using the ASC-ODE framework and the above time-steppers.

② For each method and each τ, we solve the mass–spring system on \([0,8\pi]\) and write CSV files ex19_4_rk2.csv ex19_4_rk4.csv ex19_4_irk_gauss2.csv``ex19_4_radau2a.csv

  1. Postprocessing / plotting

① plot_RK_methods.py: time evolution and phase plots for each τ.

② plot_RK_errors.py: error vs time, using the exact solution (y(t)=\cos t), (v(t)=-\sin t).

Plots#

Below we summarize the key graphical outputs (only representative examples are shown; full set available in the repository).

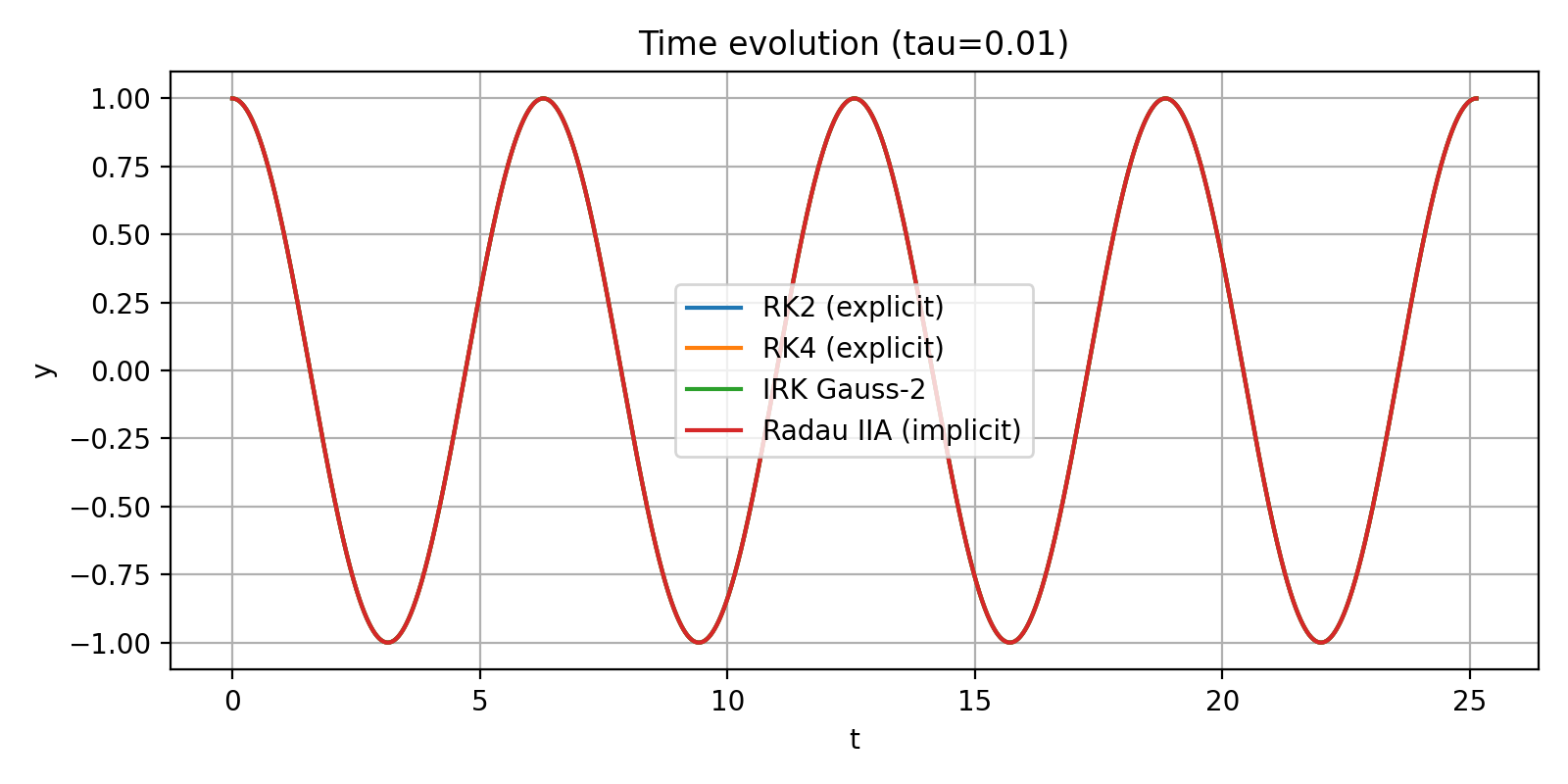
Plot 1 — Time Evolution (τ = 0.01)

All four methods overlap almost perfectly.
Small step size ⇒ high accuracy for all methods; the oscillation keeps correct amplitude and phase.

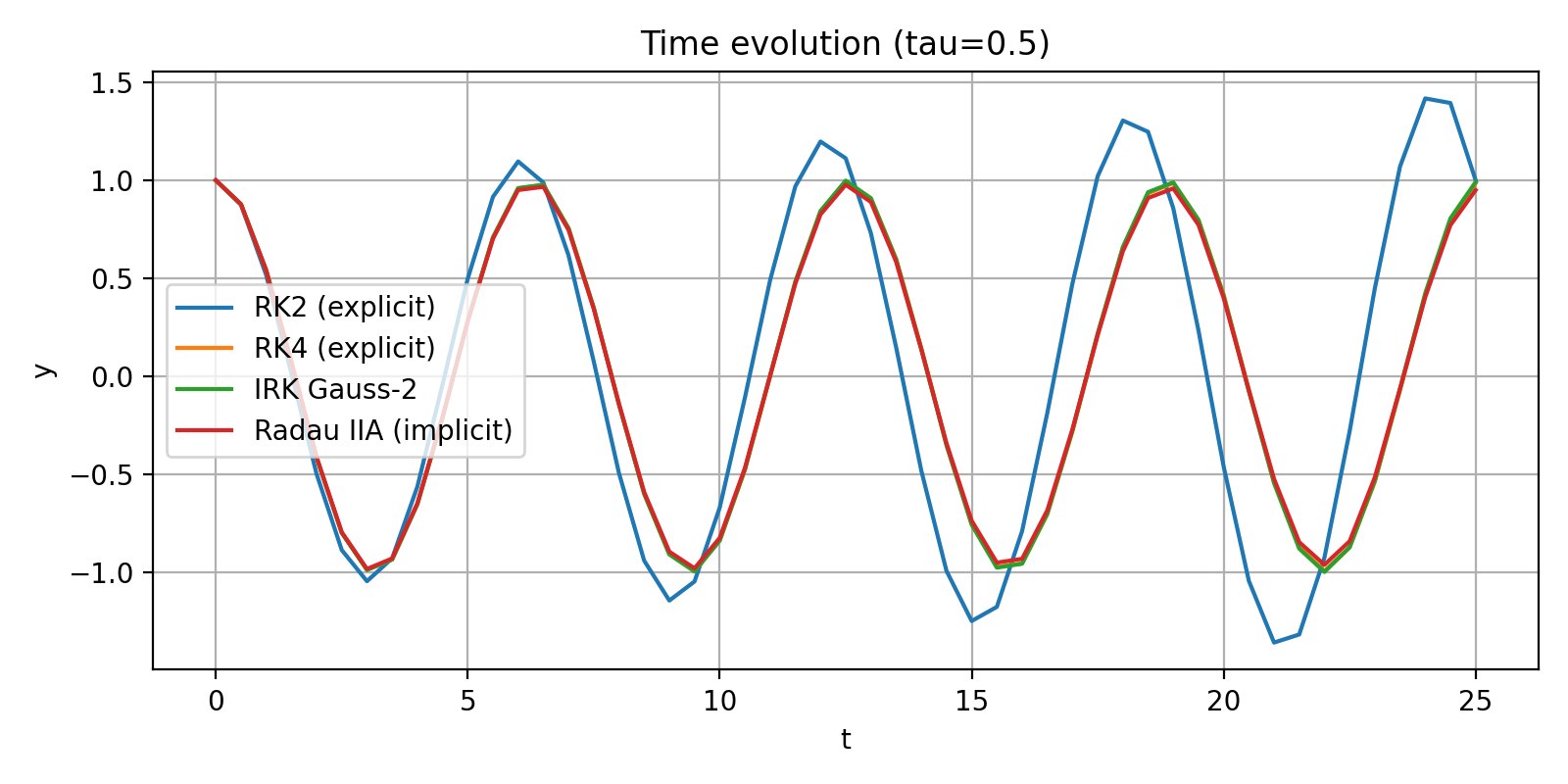
Plot 2 — Time Evolution (τ = 0.5)

Differences become visible:

  • RK2 starts to lose phase accuracy and amplitude.

  • RK4 performs better, but a small phase drift appears.

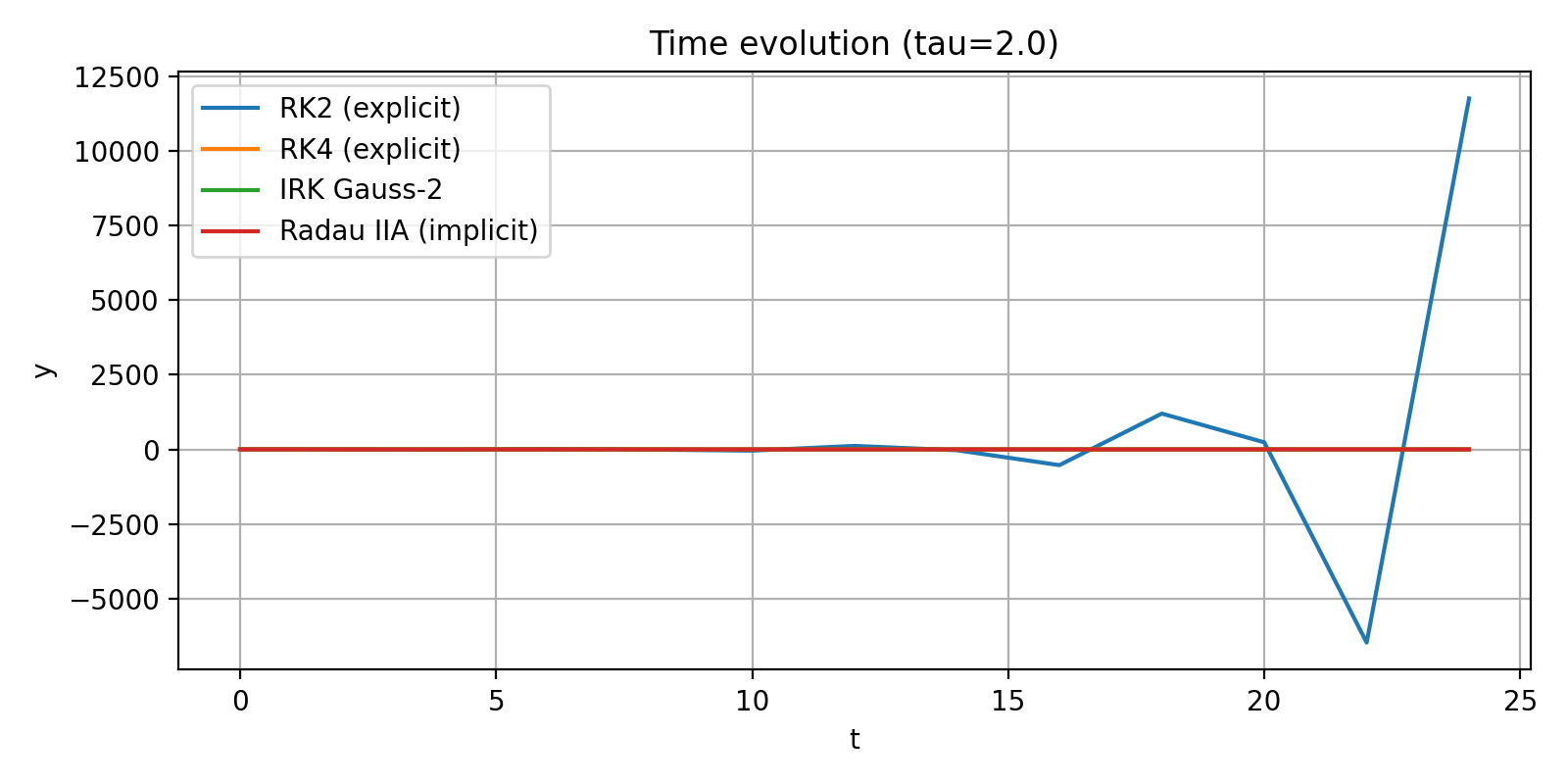
  • Gauss–Legendre and Radau IIA remain stable and stay close to the true oscillation. alt text

Plot 3 — Time Evolution (τ = 2.0)

  • RK2 becomes completely unstable and diverges.

  • RK4 already shows strong distortion.

  • Radau IIA heavily damps the oscillation (L-stable behavior).

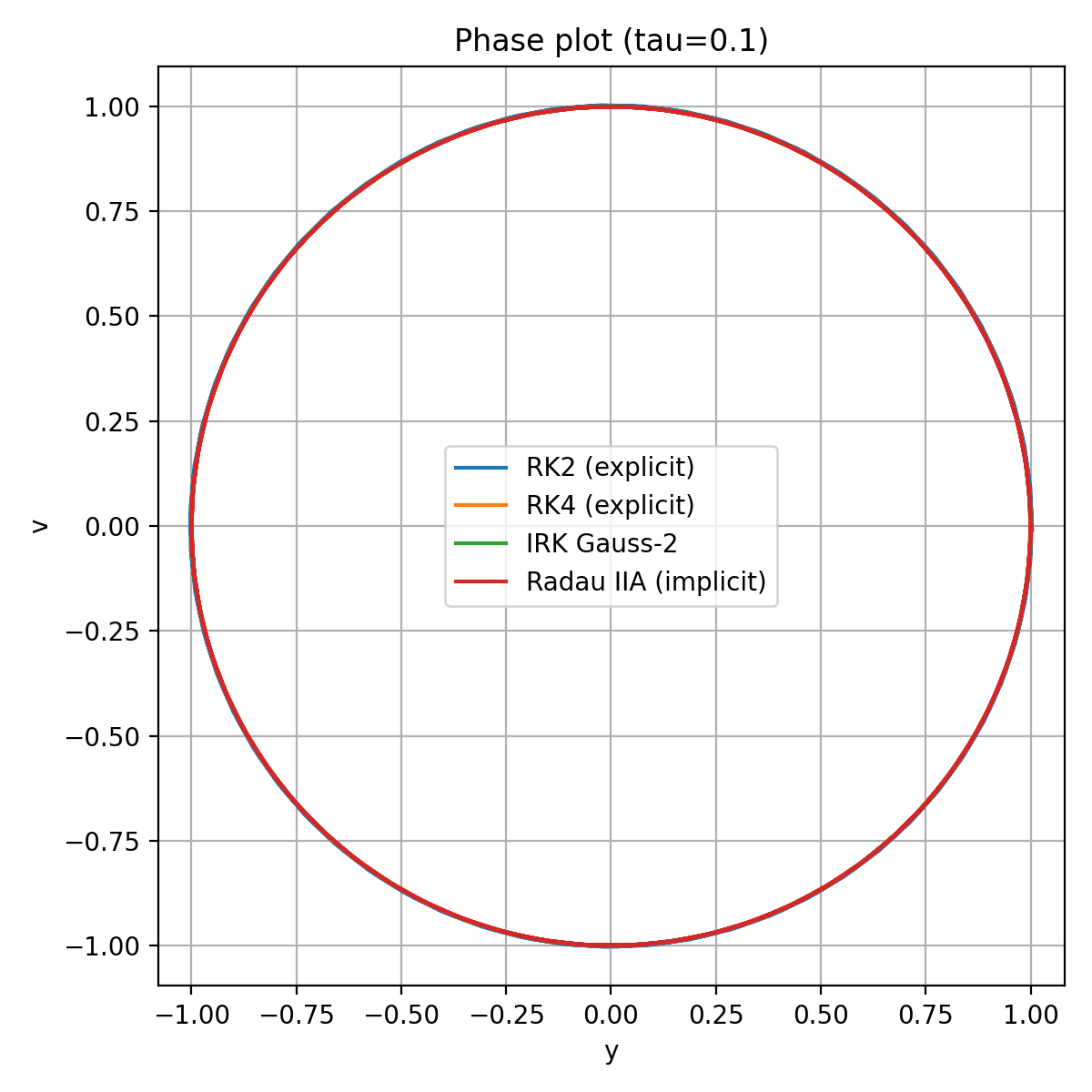
  • Gauss–Legendre remains bounded but with reduced accuracy due to the very large τ. alt text

Plot 4 — Phase Portraits (τ = 0.01)

All methods produce nearly perfect circular phase trajectories.
This corresponds to almost energy-conserving behavior at small τ.

alt text

Plot 5 — Phase Portraits (τ = 0.5)

  • RK2 spirals outward ⇒ artificial energy gain.

  • RK4, Gauss–2, and Radau IIA stay close to the exact circle; trajectories remain bounded. alt text

Plot 6 — Phase Portraits (τ = 2.0)

  • RK2 spirals dramatically outward (complete loss of stability).

  • RK4 still oscillatory but clearly distorted.

  • Gauss–Legendre stays bounded.

  • Radau IIA spirals inward due to numerical damping (L-stability). alt text

Plot 7 — Error vs Time

For each τ, the error is computed as
$\( \text{err}(t) = \big\|\,(y_{\text{num}}(t),v_{\text{num}}(t)) - (\cos t,-\sin t)\,\big\|. \)$

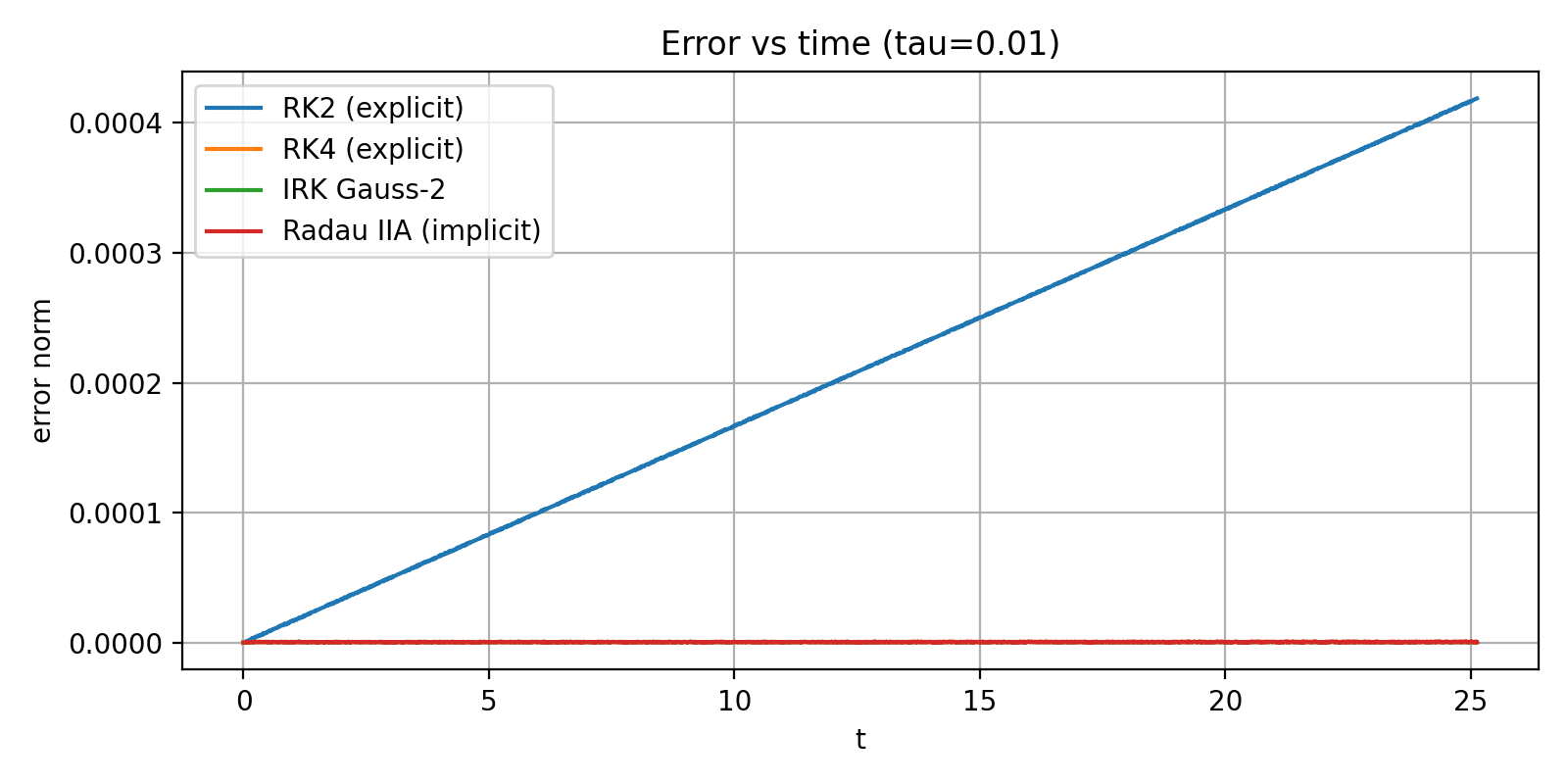
τ = 0.01 and τ = 0.1

  • RK2: small but steadily growing error.

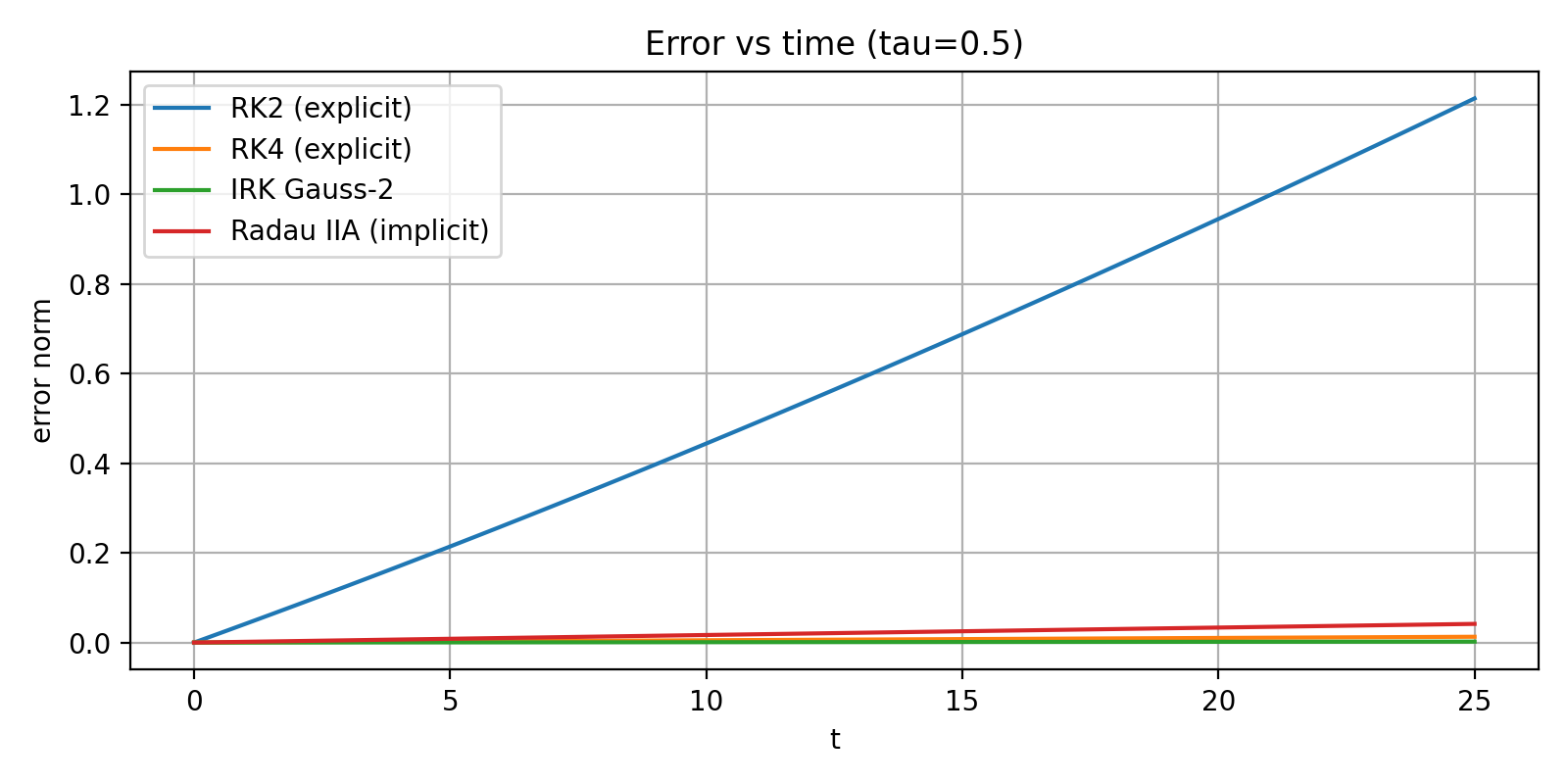
  • RK4, Gauss–2, Radau IIA: extremely small errors; curves almost coincide. alt text alt text

τ = 0.5

  • RK2: error of order O(1) over the time interval.

  • RK4: mild growth, still acceptable.

  • Gauss–2 and Radau IIA: error stays very small and almost bounded.

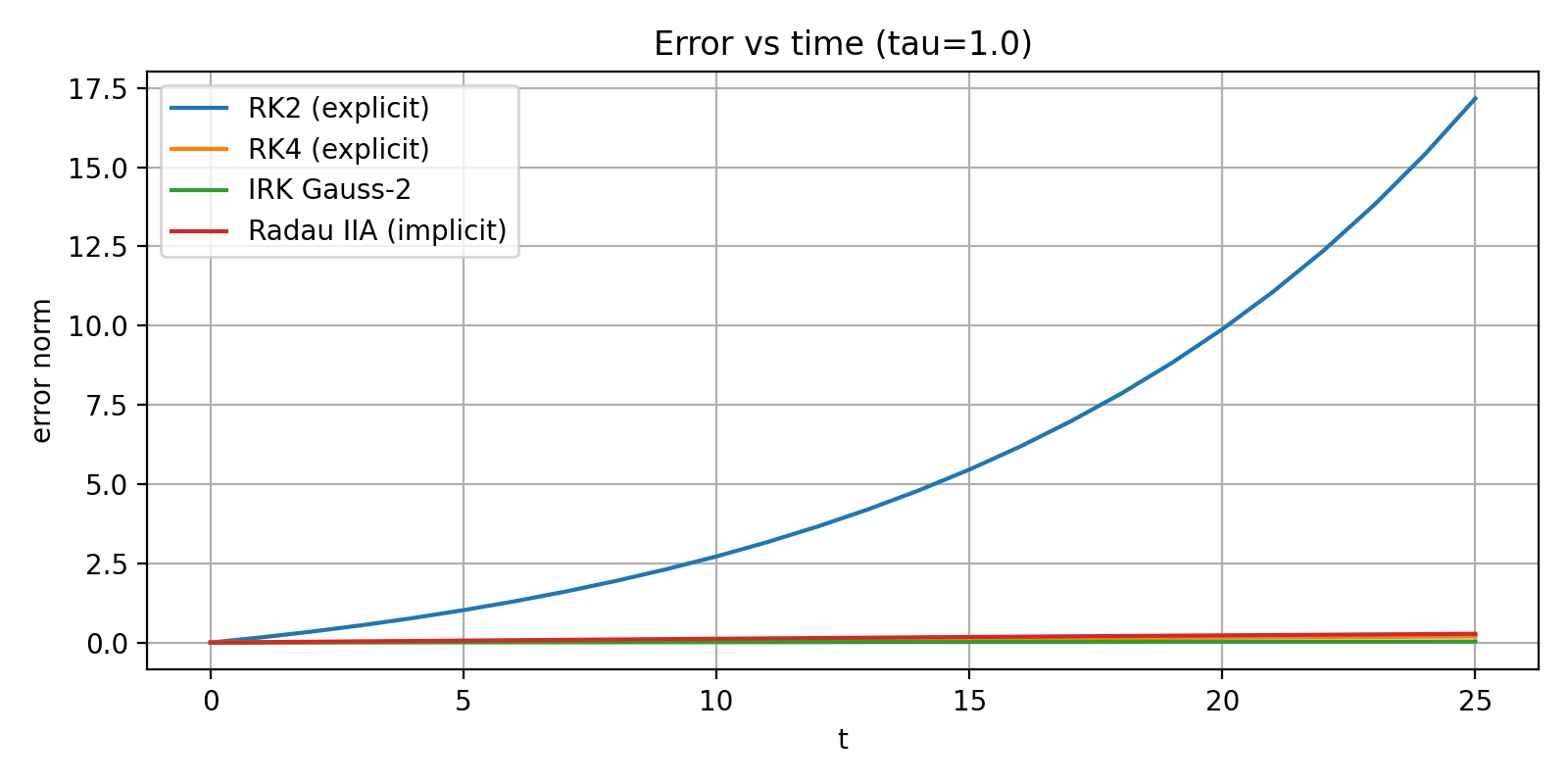
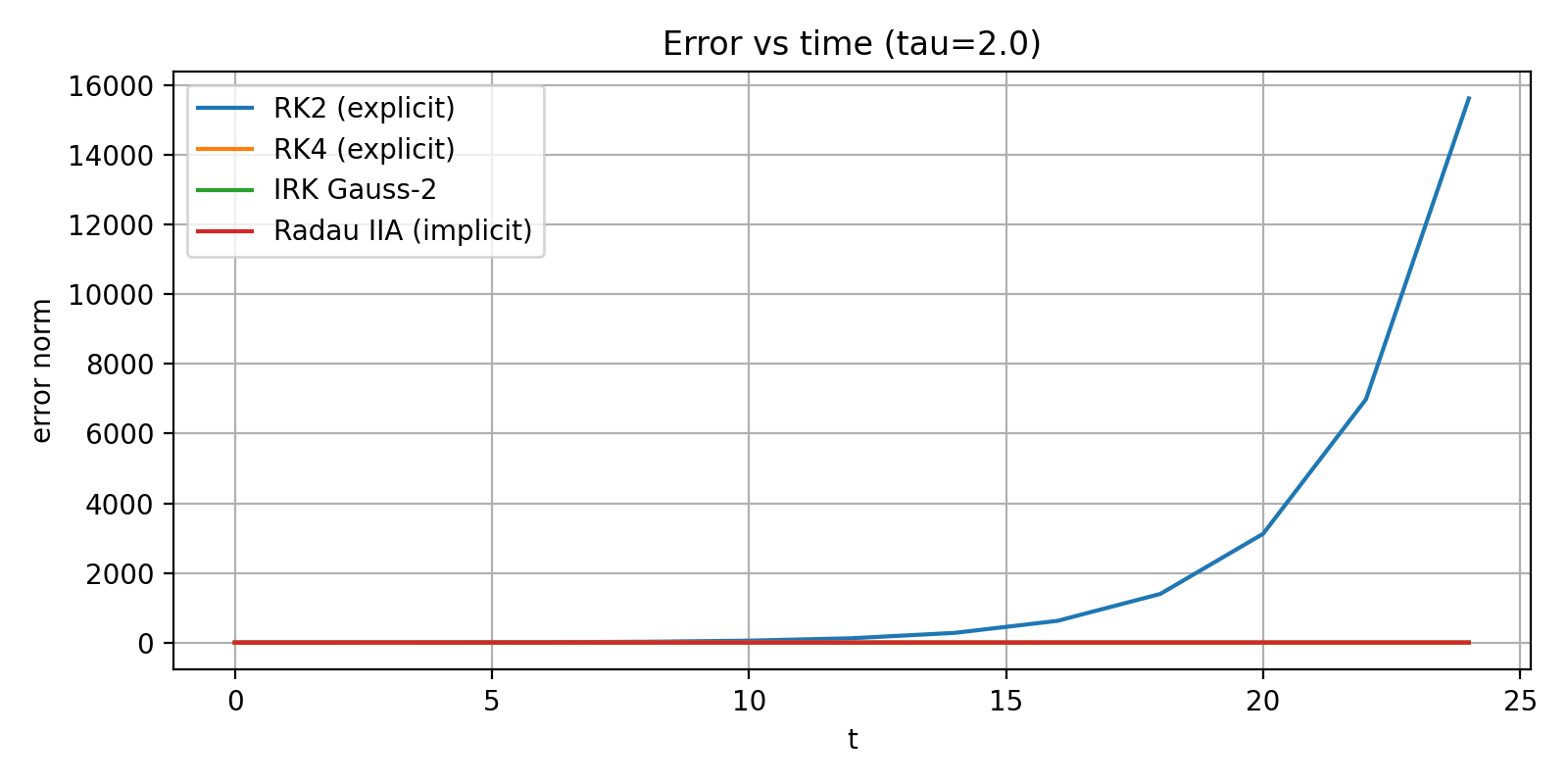
alt text

τ = 1.0 and τ = 2.0

  • RK2: error grows catastrophically (instability).

  • RK4: significant drift but still bounded.

  • Gauss–Legendre: stable with moderate error.

  • Radau IIA: best stability; error remains small even for τ = 2.0. alt text alt text

Conclusions#

ExplicitRungeKutta implementation

  • The generic ExplicitRungeKutta time-stepper successfully handles arbitrary explicit Butcher tableaus with a lower triangular (A).

  • RK2 and RK4 are obtained only by providing their coefficients, confirming that the implementation is method-agnostic and reusable.

RK2 (Explicit Heun)

  • Second-order accuracy; works well only for small τ.

  • For τ ≥ 0.5, strong phase and amplitude errors accumulate.

  • For τ ≥ 1.0, RK2 becomes numerically unstable for the oscillatory system.

RK4 (Classical Explicit)

  • Much better long-time accuracy than RK2.

  • Still not A-stable: for very large τ, phase errors become dominant.

  • Reasonable choice for moderate τ when an explicit scheme is required.

Gauss–Legendre IRK (s=2)

  • A-stable and symplectic.

  • Preserves the qualitative structure of the oscillation very well, even for larger τ.

  • Error remains bounded for all tested step sizes; phase plots stay close to a circle.

Radau IIA IRK (s=2)

  • L-stable implicit method: damps high-frequency / stiff components.

  • Extremely robust for large τ; the solution does not blow up.

  • Shows numerical damping on this pure oscillatory problem, but has the best stability among all tested methods.

Contents