Exercise 18.5

Exercise 18.5#

AutoDiff Pendulum

Overall Process#

  1. Adapted the C++ file ex18_5.cpp to simulate the nonlinear pendulum using

\[ \dot{\theta} = \omega,\qquad \dot{\omega} = -\frac{g}{L}\sin(\theta) \]

with AutoDiff-based Jacobian evaluation.

  1. Generated output trajectory file:
    ex18_5.csv

  2. Created Python scripts to plot:

    • pendulum_time.png — Time evolution of θ(t) and ω(t)

    • pendulum_phase.png — Phase portrait (θ vs ω)

Plots#

Plot 1 – Time Evolution of Pendulum (Explicit Euler)#

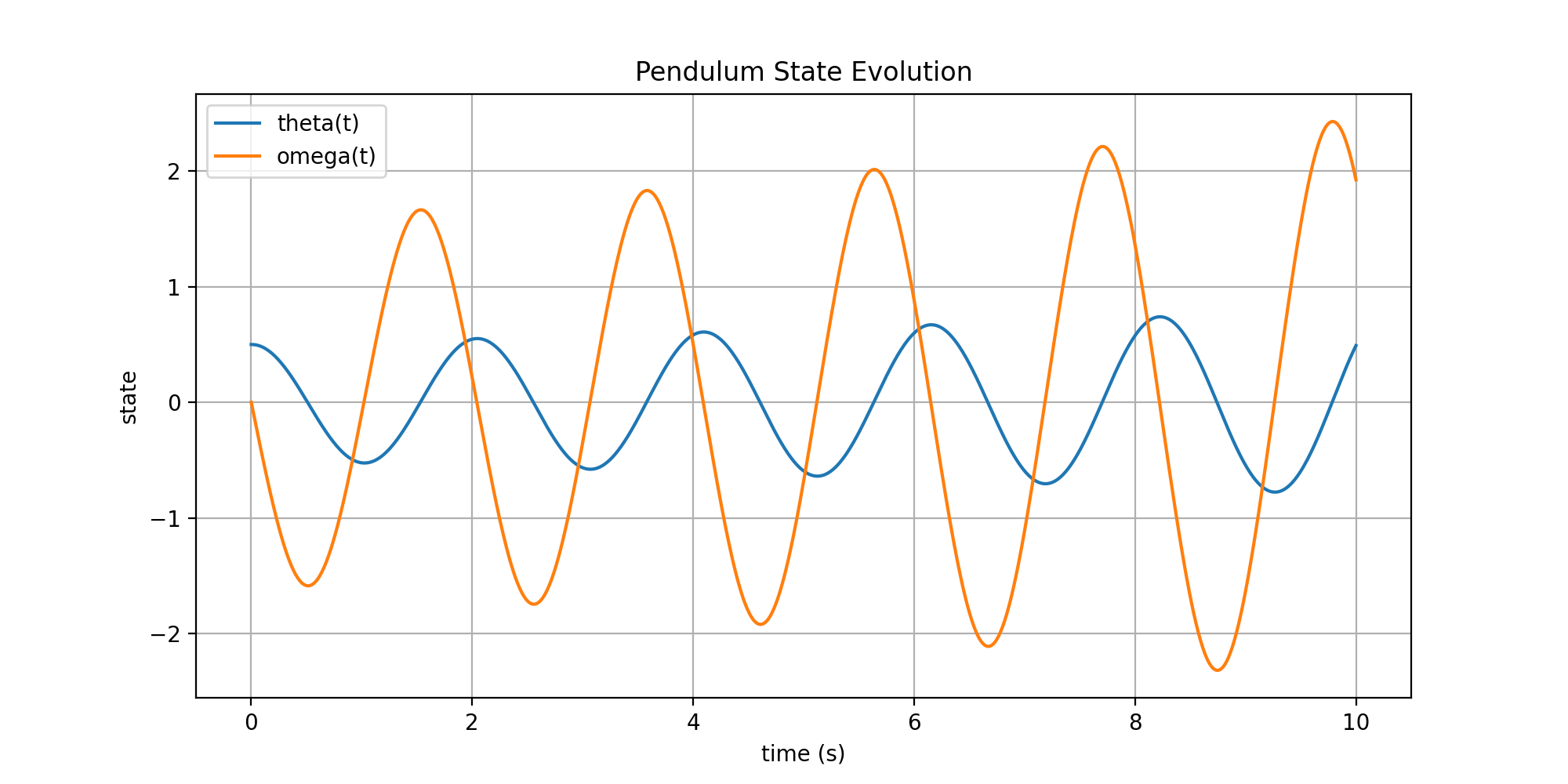
Time Evolution

This plot shows the temporal evolution of the pendulum state variables:

  • θ(t) : angular displacement

  • ω(t) : angular velocity

Euler integration introduces numerical energy growth over time.

Plot 2 – Phase Plot (Explicit Euler)#

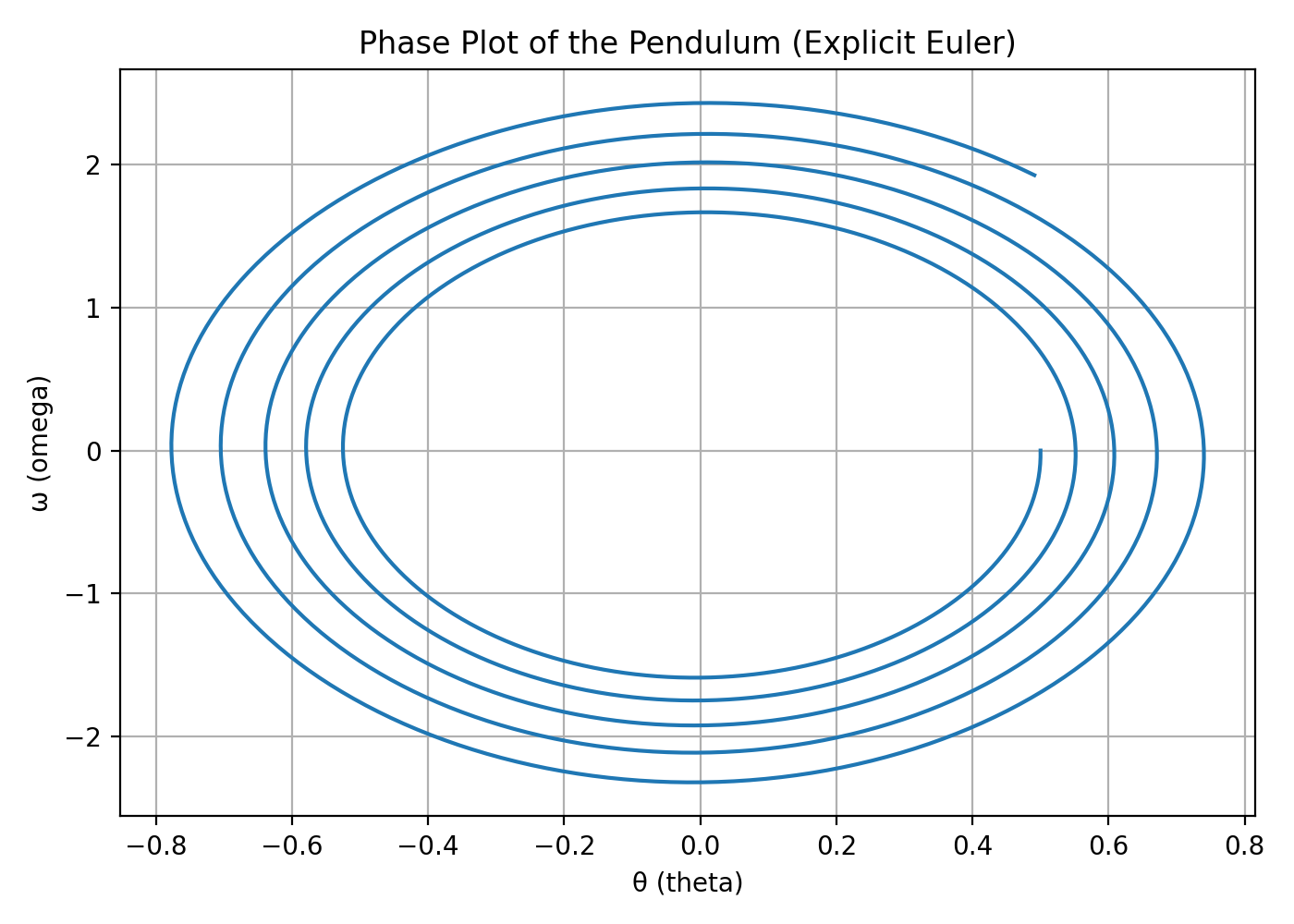
Phase Plot

This is the θ–ω phase portrait of the nonlinear pendulum.
A true physical pendulum would trace closed orbits (constant energy), but explicit Euler causes energy to drift.

Conclusion#

  • The explicit Euler method behaves numerically unstable for oscillatory systems like the pendulum.

  • The time evolution plot shows that both \( \theta(t) \) and \(\omega(t)\) exhibit increasing amplitude, indicating energy gain.

  • The phase portrait spirals outward instead of forming closed loops:

    • This means energy is not conserved numerically.

    • The trajectory grows unphysically over time.

  • AutoDiff successfully computes Jacobians for the nonlinear pendulum model.

Contents