Exercise 17.4.1

Exercise 17.4.1#

Q1 : Overall Process#

Adapted Implicit_Euler.cpp to get implicit_euler.csv. Then adapted plotq2.1.py and get graph plot5 and plot6.

Q1 : Plot#

Plot 5 : Time Evolution (implicit euler)#

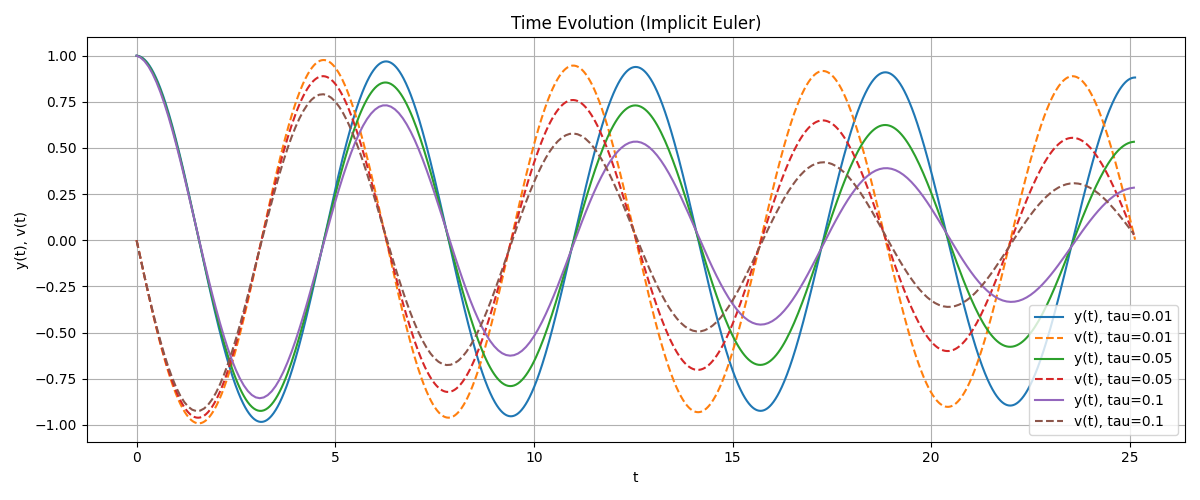
Plot 5 : Time Evolution

Plot 6 : Phase Plots (implicit euler)#

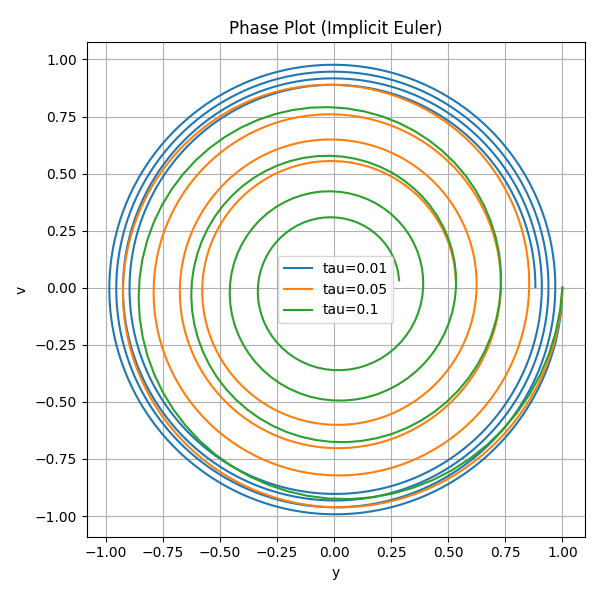
Plot 6 : Phase Plots

Q2 : Overall Process#

  1. The general function of Crank-Nicolson method is:

 u_{n+1} - u_n - (tau/2)*(f(u_{n+1}) + f(u_n)) = 0

  1. Adapted Crank_Nicolson.cpp to get crank_nicolson.csv. Then adapted plotq2.2.py and get graph plot7 and plot8.

Q2 : Plot#

Plot 5 : Time Evolution (Crank-Nicolson)#

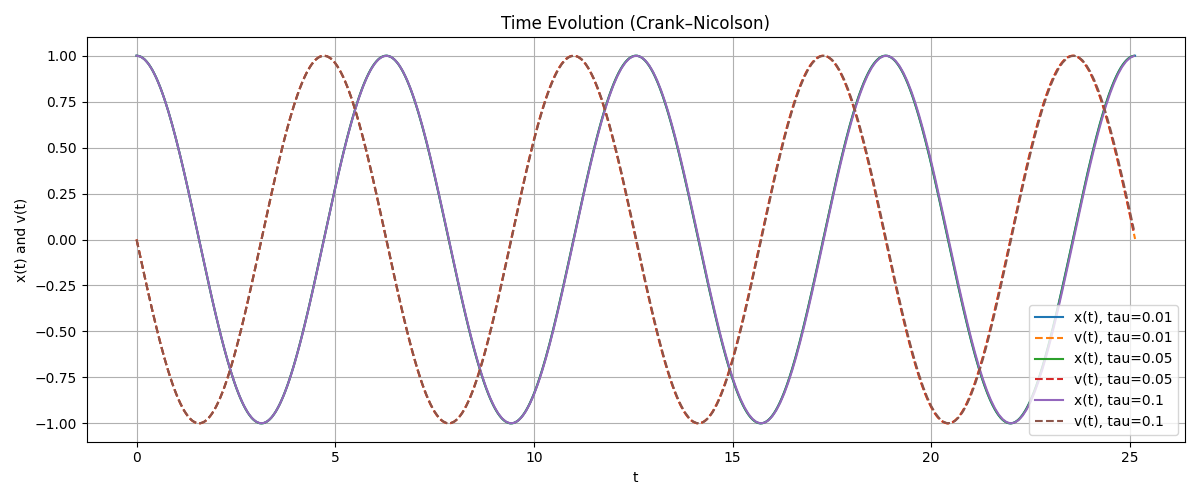
Plot 7 : Time Evolution

Plot 6 : Phase Plots (Crank-Nicolson)#

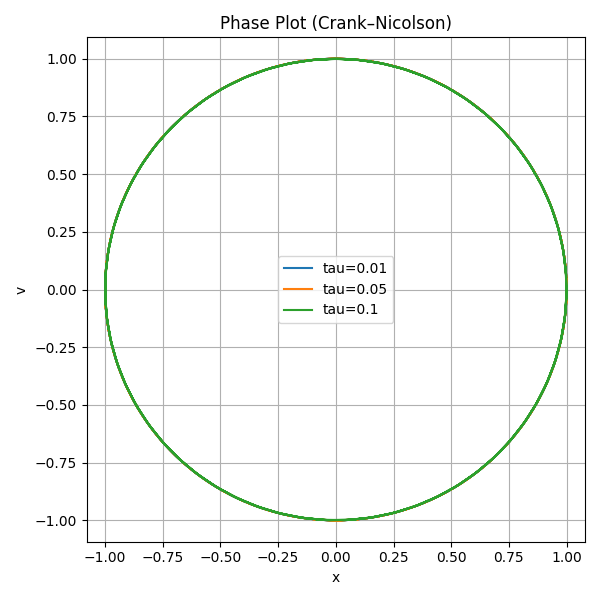
Plot 8 : Phase Plots

Q3 : Comparison of the Four Time-Stepping Methods#

Now we compare 4 methods in previously mentioned:

Explicit Euler

  • The method is unstable for oscillatory systems.

  • For moderate or even small time-steps, the numerical orbit in the phase plane spirals outward, corresponding to an artificial gain of energy.

  • Larger time-steps lead to very rapid divergence.

Improved Euler

  • Shows second-order accuracy and significantly better behavior.

  • The phase curves stay close to a circle, even for larger time-steps.

  • There is still a small drift, but the energy error remains bounded and does not grow dramatically like in Explicit Euler.

Implicit Euler

  • Always stable, regardless of time-step size.

  • However, the solution exhibits numerical damping: the phase orbit spirals inward, meaning the method artificially removes energy from the system.

Crank–Nicolson

  • It is the one given the best results. Always stable, and energy-preserving method for linear oscillatory systems.

  • The phase plots remain almost perfectly circular for all tested time-steps.

In General: 
For oscillatory systems -- the mass–spring model, Crank–Nicolson provides the most physically accurate long-time behavior, while Explicit Euler is the worst method.
Contents