Exercise 18.4

Exercise 18.4#

Q1 & Q2: Implementation of AutoDiff Class. Overall Process.#

  1. Extended the provided autodiff.hpp library to include additional useful operators. Specifically, subtraction (operator-), negative sign operator and division (operator/) by applying the quotient rule.

  2. Added some more mathematical functions like cos, exp and log that accept AutoDiff variables and computed correctly its derivatives by implementing the chain rule.

  3. Verified the correctness of these new operators using demo_autodiff_new.cpp.

Q3: Legendre- Polynomials. Overall process.#

  1. Implemented the recursive formula to compute Legendre-polynomials. Since our AutoDiff class supports templates, the same function calculates both values and derivatives:

    P[k] = ((T(2 * k - 1) * x * P[k - 1]) - T(k - 1) * P[k - 2]) / T(k);

  2. Created test_legendre.cpp to generate data (with step 0.02) for Legendre-polynomials up to order \(n=5\) in the interval \([-1, 1]\).

  3. Created the python script plot_combined.py to visualize the family of polynomials and their derivatives.

Q3: Plots#

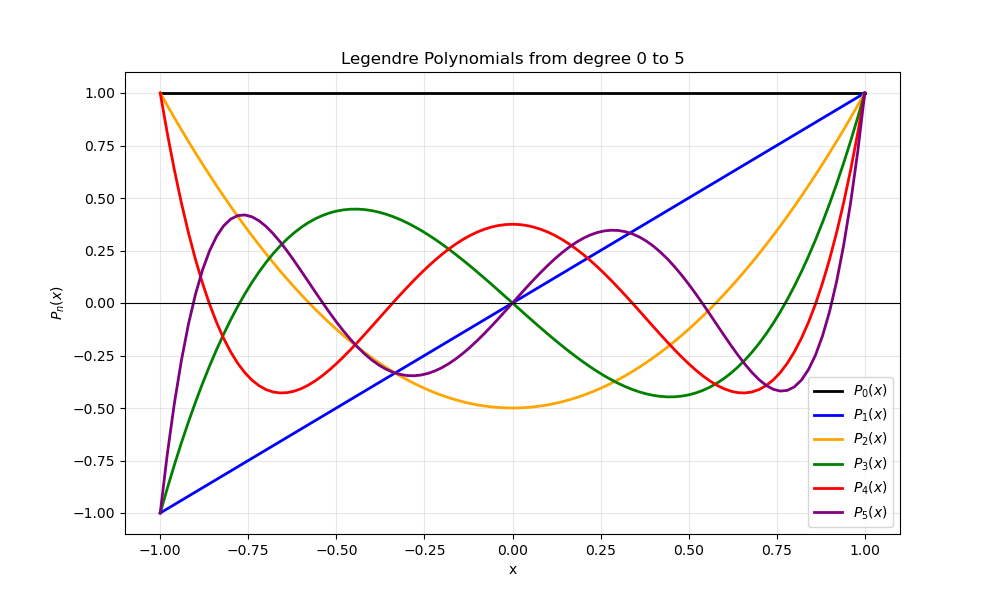
Plot 1: Legendre-Polynomials (Orders 0 to 5)#

Legendre Polynomials Family

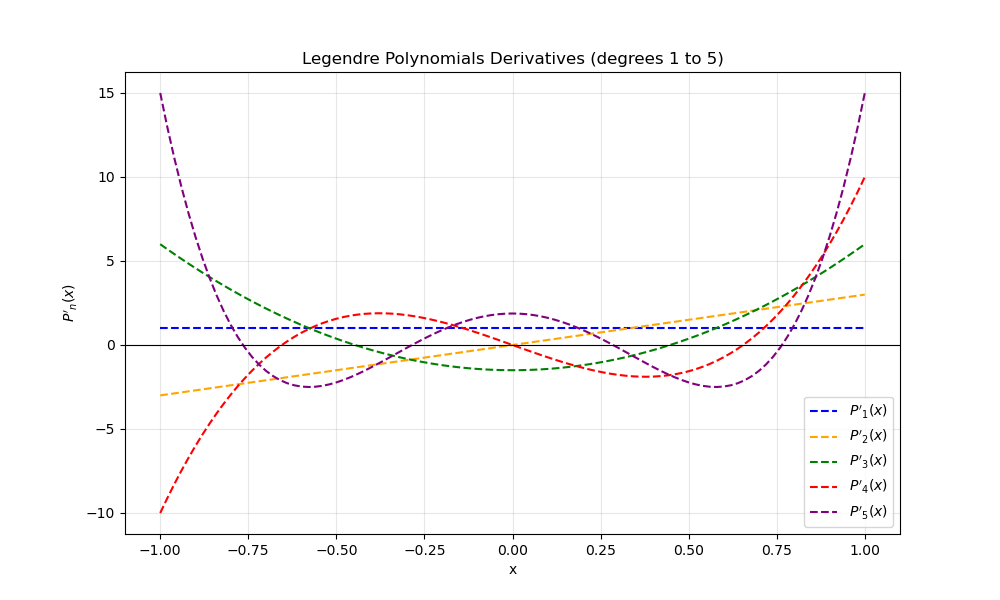
Plot 2: Legendre-Polynomials Derivatives (Orders 1 to 5)#

Note: Derivative of the Polynomial or order 0 is not shown because its value is 0, so plotting it would make the graphic much smaller to show that horizontal line at 0 making it difficult to see the other polynomials derivative values.

Legendre Derivatives Family

Q3: Conclusion#

  • As seen in Plot 1, all polynomials strictly satisfy the theoretical condition \(P_n(1) = 1\), confirming the numerical stability of the recursive implementation.

  • Parity and Symmetry: The plots show the parity properties of Legendre-polynomials:

    • Even orders (\(P_0, P_2, P_4\)) are symmetric about the Y-axis (even functions).

    • Odd orders (\(P_1, P_3, P_5\)) are antisymmetric (odd functions), satisfying \(P_n(-1) = -1\).

  • Derivative Behavior: Plot 2 shows that derivatives oscillate with increasing amplitude near the boundaries. For the order 5 polynomial, the derivative at \(x=1\) take the value 15 which is the theoretical prediction \(P'_n(1) = \frac{n(n+1)}{2}\).

  • The derivative inverts the parity: for an even polynomial, \(P'_n\) becomes an odd function (crossing zero at the origin) and vice versa.

Contents