Exercise 17.4.1

Q4: Question Review

We already have the main funtion

\[ U_c(t) + RC\,\frac{dU_C}{dt} = U_0(t) \]

with initial condition: \(U_c(0) = U_0(0)\)

and assumption:

1. \(U_c(t)\) is the unknown quantity

2. \(U_0(t) = cos(100*pi*t)\)

3. R = 100

4. C = \( 10 ^{-6}\)

Q4.1 : Rewrite the system to antonomous form

We see that in the function, there are some terms realted to t. Now we define a new vector:

\[ x_1 = U_c(t), x_2 = t \]

then the new vecotr:

\[\begin{split} x = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \end{split}\]

Finally we get the autonomous ODE:

\[ \dot{x}_1 = \frac{1}{RC}\left(\cos(100\pi x_2) - x_1\right) \]

\[ \dot{x}_2 = 1 \]

with initial value

\[ x_1(0) = U_0(0) = 1, \qquad x_2(0) = 0 \]

Q4.2 : Numerically solve the problem with 3 methods

In order to compare the methods: Explicit Euler, Implicit Euler and Crank Nilcolson method, add three head files: RCRHC.hpp RCCircuit.hpp and RHS.hpp

Modify the previous main document, change the model from mass-spring to RC circuit. The main files are xian.cpp yin.cpp and cn.cpp. After getting the csv files, plot and analyze.

Attention: Here we choose different step N = {50, 100, 200,300} and T = 0.2 to compare. In this case, the explicit method is not stable and the numerical solution blows up. So we put explicit euler method seperately and add log-log plot to see the error.

Plot

Explicit Euler method in different time step (BLOW UP)

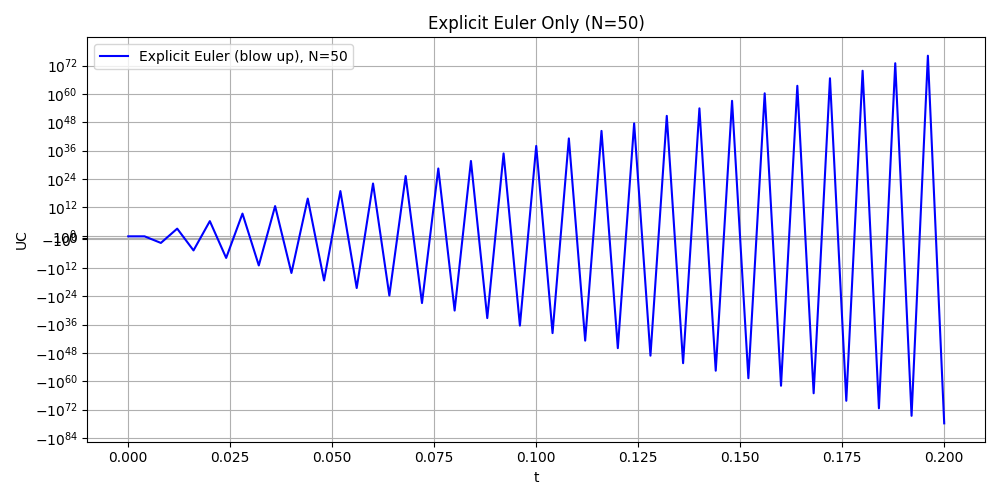
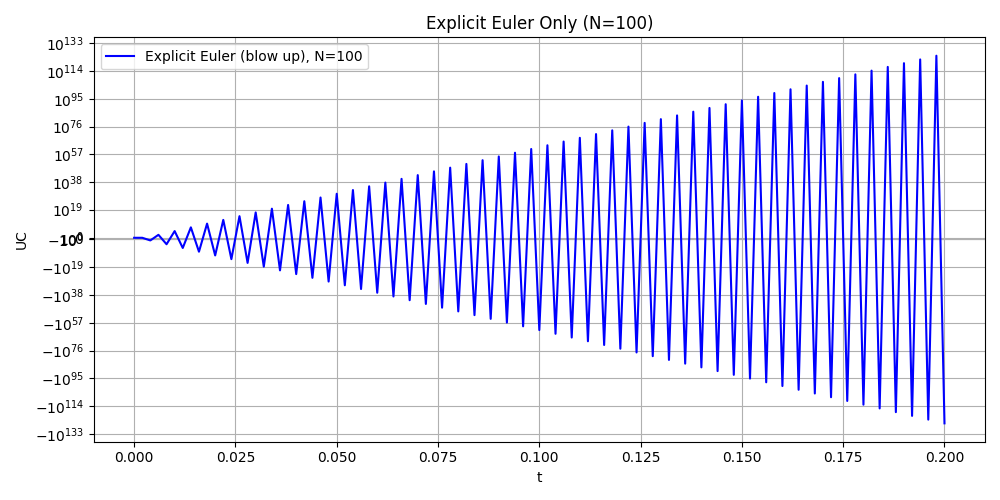
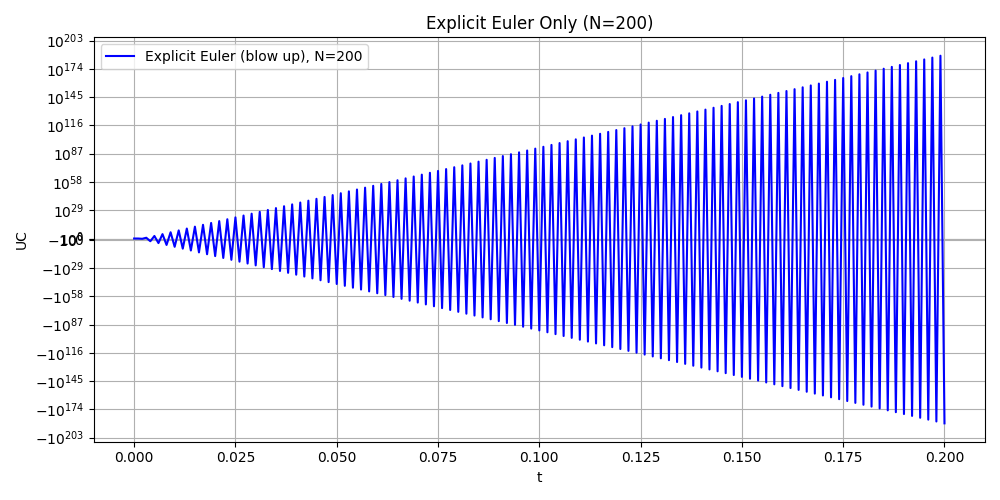
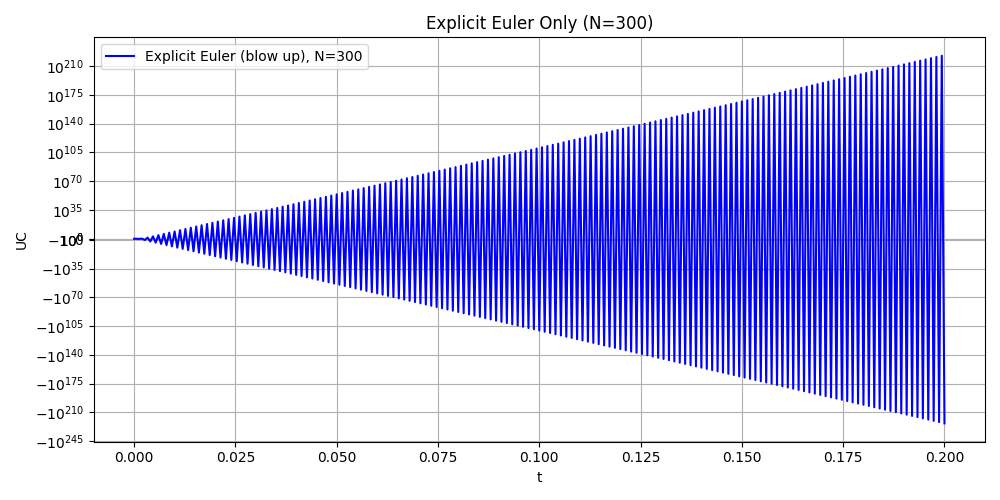
Implicit Euler vs Crank Nicolson in different time step

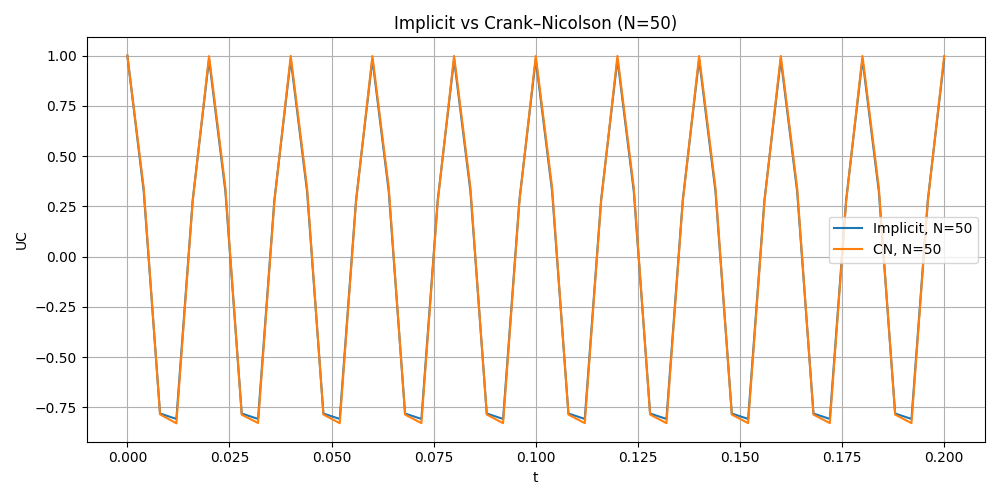
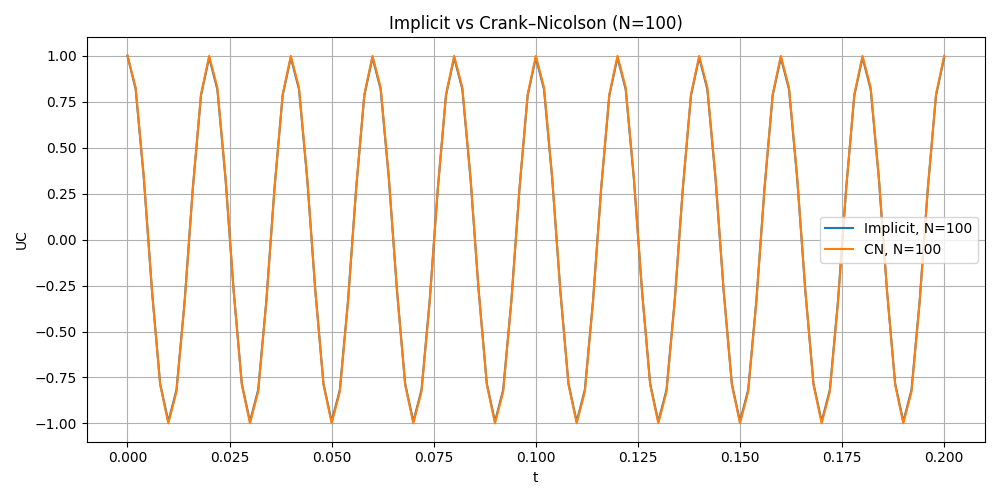
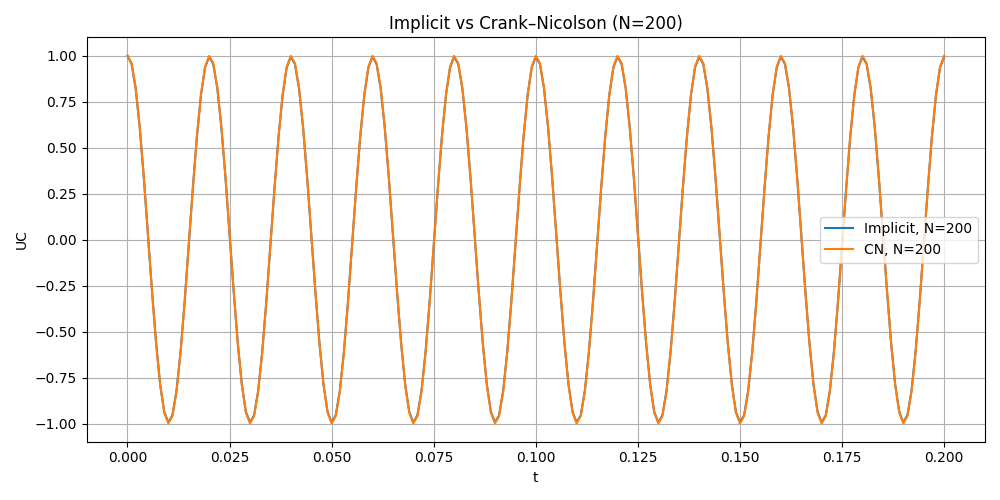
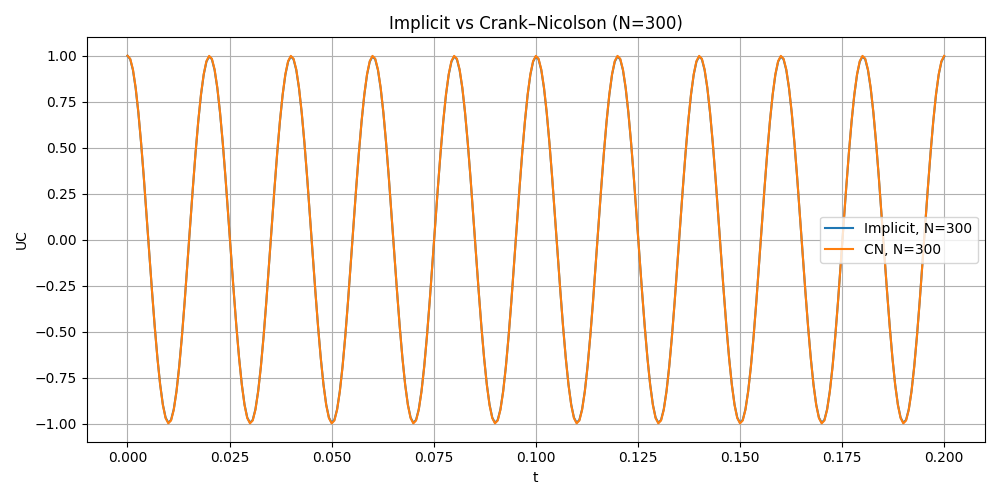
Error Analysis

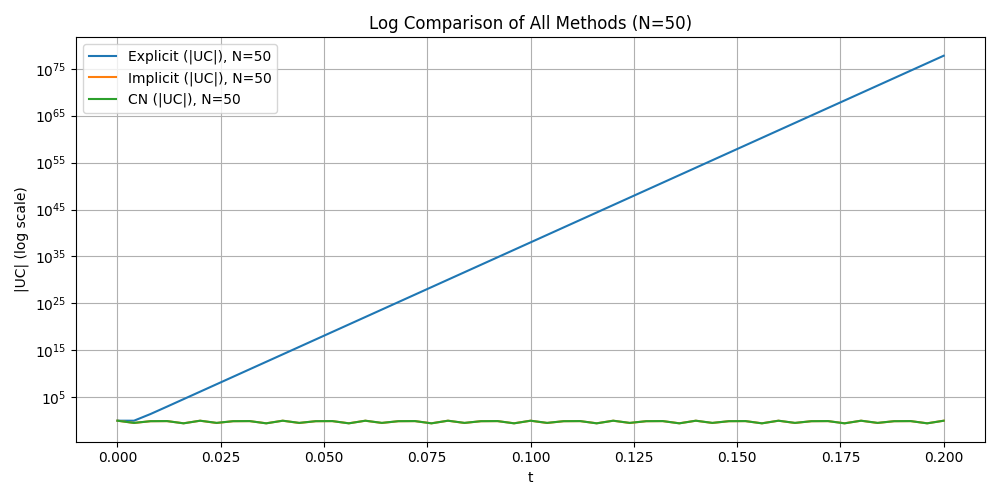
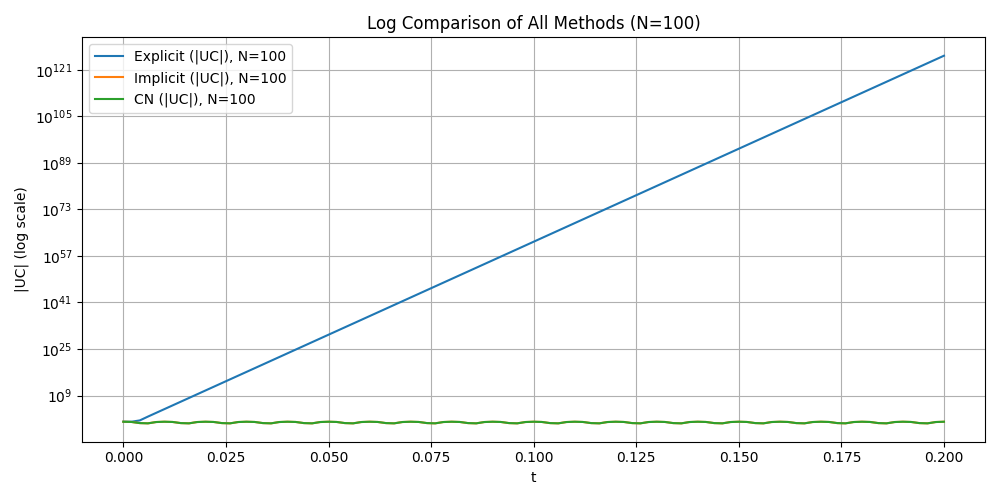
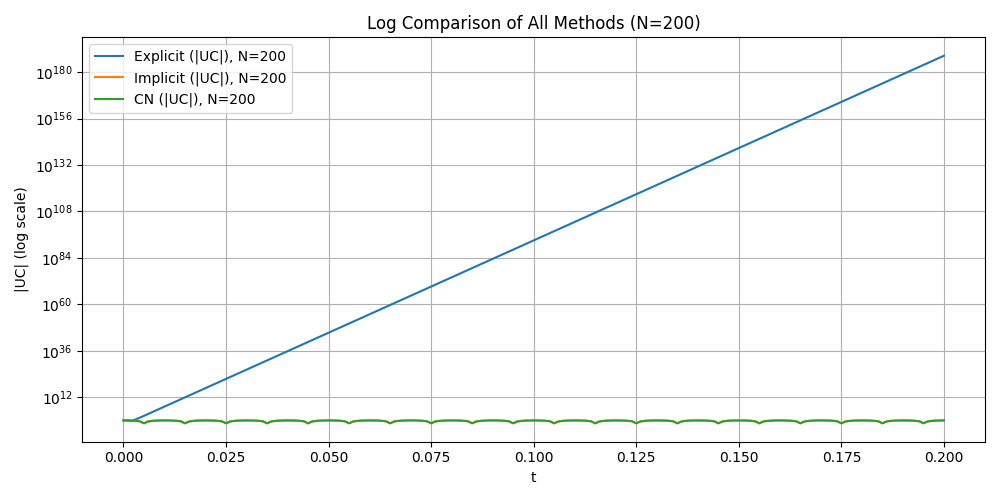
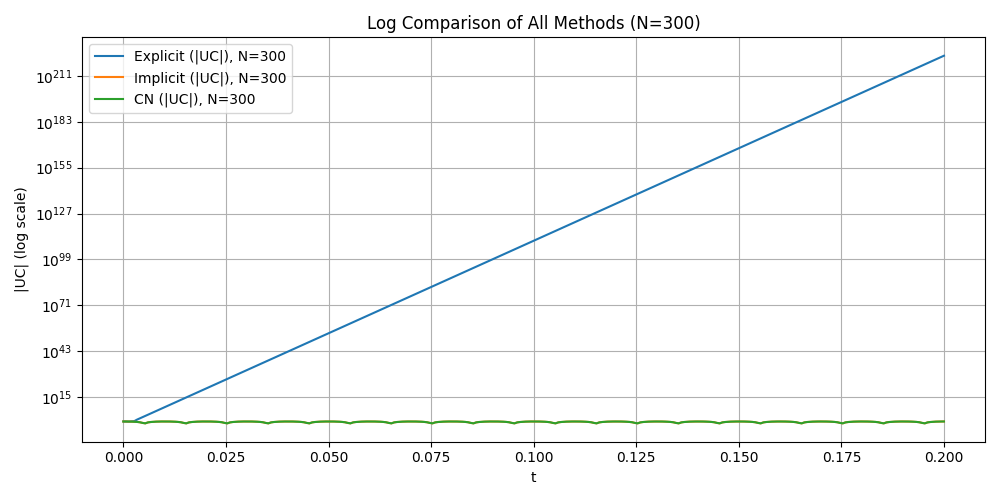
Conclusion

• Explicit Euler is unstable for the RC circuit. The step sizes Δ𝑡=𝑇/𝑁 violate the stability limit Δ𝑡<2𝑅𝐶, leading to rapid blow-up.

• Implicit Euler is stable but overly damped. As an A-stable first-order method, it does not diverge, but it introduces strong numerical dissipation.

• Crank–Nicolson gives the best results. It is A-stable, second-order accurate, and preserves oscillation amplitude without artificial damping.

• Convergence behavior: Explicit Euler → 1st order (unstable here) Implicit Euler → 1st order (stable but dissipative) Crank–Nicolson → 2nd order (accurate and stable)

Overall: For this stiff RC system, Crank–Nicolson is the best method.